LCM Cardinality

Each pair of integers has a unique LCM:
lcm(a, b) = a * b / gcd(a, b)
Note that gcd(a, b) is unque too.
The LCM cardinality for an integer (n) is the number of distinct pairs of integers (a & b) that satisfy:
n = lcm(a, b)
A few Examples:

6	8	9	12
=====	=====	=====	=====
1, 6	1, 8	1, 9	1, 12
2, 6	2, 8	3, 9	2, 12
3, 6	4, 8	9, 9	3, 12
6, 6	8, 8	-----	4, 12
-----	-----	3, 3	6, 12
2, 3	2, 4		12,12
			-----
			2, 6
			3, 4
=====	=====	=====	=====
5	5	4	8

After observing the pattern, what we’re actually doing is: we are counting the number of factors of the integer n, HOWEVER, factors less than or equal to the root of n are counted twice (except the factor 1).
For example the cardinality of 16:

factor			1	2	4	8	16
factor <= 4		true	true	true	false	false
lcm cardinality	=	1 +	2 +	2 +	1 +	1	= 7

We can implement this either with pre-calculation or factorization.

Pre-calculation

#include <iostream>
#include <climits>
#include <cstdlib>
using namespace std;

const int N = 5000;
int lcmCardinality[N];

void calculate() {
	// 1
	lcmCardinality[1] = 1;
	for (int i = 2; i < N; ++i)
		lcmCardinality[i] = 0;
	// other
	for (int i = 2; i < N; ++i) {
		// less than root
		for (int j = i; j <= i * i && j <= N; j += i)
			lcmCardinality[j] += 2;
		// more
		if (i + 1 < INT_MAX / i)
			for (int j = i * (i + 1); j <= N; j += i)
				lcmCardinality[j]++;
	}
}

int main() {
	calculate();
	int n;
	while (cin >> n)
		cout << lcmCardinality[n] << endl;
	return 0;
}

11321 – Sort! Sort!! and Sort!!!

A simple sort problem with a weird sort criterion.
Caution!

• Be careful with odd/even check on negative numbers.

C++ implementation with rank 315:

#include <cstdio>
#include <algorithm>
using namespace std;

typedef long long int64;
#define N 10000

int64 lst[N], n, m;

bool cmp(int64 a, int64 b) {
	if (a % m != b % m) return a % m < b % m;
	int64 absA = abs(a), absB = abs(b);
	if (absA % 2 == 1 && absB % 2 == 0) return true;
	if (absA % 2 == 0 && absB % 2 == 1) return false;
	if (absA % 2 == 1 && absB % 2 == 1) return a > b;
	if (absA % 2 == 0 && absB % 2 == 0) return a < b;
	return false;
}

int main() {
	while (scanf("%lld %lld", &n, &m) == 2 && n && m) {
		printf("%lld %lld\n", n, m);
		for (int64 j = 0; j < n; ++j)
			scanf("%lld", &lst[j]);
		sort(lst, lst + n, cmp);
		for (int64 j = 0; j < n; ++j)
			printf("%lld\n", lst[j]);
	}
	printf("0 0\n");
	return 0;
}

530 – Binomial Showdown

This problem is identical to 369 – Combinations.

369 – Combinations

A combinations problem. Given N and R, find NCR.
There’s a variety of ways; The first two solutions are straight-forward computation of 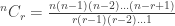. The last two have some tricks:

A naive Java solution that uses big arithmetic:

import java.math.*;
import java.util.*;

public class Main {

	private static BigInteger C(BigInteger n, BigInteger r) {
		r = (r.compareTo(n.subtract(r)) > 0) ? n.subtract(r) : r;
		BigInteger num = BigInteger.ONE, den = BigInteger.ONE;
		while (!r.equals(BigInteger.ZERO)) {
			num = num.multiply(n); den = den.multiply(r);
			r = r.subtract(BigInteger.ONE); n = n.subtract(BigInteger.ONE);
		}
		return num.divide(den);
	}

	public static void main(String[] args) {
		Scanner s = new Scanner(System.in);
		while (s.hasNext()) {
			BigInteger n = s.nextBigInteger(), r = s.nextBigInteger();
			if (n.equals(BigInteger.ZERO) && r.equals(BigInteger.ZERO))
				break;
			System.out.printf("%s things taken %s at a time is %s exactly.\n", n, r, C(n, r));
		}
	}
}

A similar C++ solution:

#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;

unsigned long long C(int n, int r) {
	r = min(n - r, r);
	long long out = 1;
	for (int i = 1; i <= r; ++i) {
		out *= n - r + i;
		out /= i;
	}
	return out;
}

int main() {
	long long n, r;
	while (scanf("%lld %lld", &n, &r) == 2 && n && r)
		printf("%lld things taken %lld at a time is %lld exactly.\n", n, r, C(n, r));
	return 0;
}

A slower, but totally accepted, solution reduces the computations as you were doing it by hand; We have two arrays, one for the numerator and another for the denominator. We do a 2D loop to reduce the numerator with respect to the denominator and hence the answer. C++ implementation:

#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
using namespace std;

#define REDUCE(a, b) { int g = gcd(a, b); a /= g; b /= g; }

int num[100], den[100];
int numI, denI;

long long gcd(long long a, long long b) {
	long long t;
	while (a) { t = a; a = b % a; b = t; }
	return b;
}

long long C(int n, int r) {
	// fill arrays
	r = min(n - r, r);
	numI = denI = 0;
	while (r) { num[numI++] = n--; den[denI++] = r--; }
	// reduce & compute
	long long out = 1;
	for (int i = 0; i < numI; ++i) {
		for (int j = 0; j < denI; ++j)
			REDUCE(num[i], den[j]);
		out *= num[i];
	}
	return out;
}

int main() {
	long long n, r;
	while (scanf("%lld %lld", &n, &r) == 2 && n && r)
		printf("%lld things taken %lld at a time is %lld exactly.\n", n, r, C(n, r));
	return 0;
}

The last solution has the same complexity as the first two. It uses Pascal’s Triangle for computing combinations. C++ implementation:

#include <cstdio>
using namespace std;

#define N 128

long long pascalTri[N * (N + 1) / 2];

void fillPascal() {
	for (int l = 0, lStart = 0; l < N; ++l, lStart += l) {
		pascalTri[lStart] = pascalTri[lStart + l] = 1;
		for (int i = 1; i < l; ++i)
			pascalTri[lStart + i] = pascalTri[lStart + i - l] + pascalTri[lStart + i - l - 1];
	}
}

int main() {
	fillPascal();
	long long n, r;
	while (scanf("%lld %lld", &n, &r) == 2 && n && r)
		printf("%lld things taken %lld at a time is %lld exactly.\n", n, r, pascalTri[n * (n + 1) / 2 + r]);
	return 0;
}

10814 – Simplifying Fractions

A simple math GCD problem with big arithmetic.

• Get fraction a / b.
• Find g : GCD(a, b).
• Divide both a, b by g.
• Output.

Rank 461 Java code:

import java.math.BigInteger;
import java.util.Scanner;

public class Main {

	private static BigInteger gcd(BigInteger a, BigInteger b) {
		BigInteger t;
		while (a.compareTo(BigInteger.ZERO) != 0) {
			t = a;
			a = b.mod(a);
			b = t;
		}
		return b;
	}

	public static void main(String[] args) {
		Scanner s = new Scanner(System.in);
		int n = s.nextInt();
		BigInteger a, b, g;
		while (n-- > 0) {
			a = s.nextBigInteger();
			s.next();
			b = s.nextBigInteger();
			g = gcd(a, b);
			System.out.println(a.divide(g) + " / " + b.divide(g));
		}
	}
}