minimum

Introduction to Segment Trees (Range Minimum Query)

March 12, 2014 by MSiddeek, posted in Algorithms, Data Structure

Range Minimum Query

Given an array $A$ of length $N$ , answer $getMin(i, j)$ qeuries. $getMin(i, j)$ should return the index $m$ , where $A[m] = min_{i<k<j}\{A[k]\}$ .

There are many ways to do this. In the case where $A$ 's element values are allowed to change, and yet we have to maintain $getMin(i, j)$ to work correctly, a segment tree is our best option. Follows is a brief explanation of segment trees for this specific example. I'll put a more generalized explanation in another post.

Segment Trees

The idea behind a segment tree is to build a binary tree where each node represents a segment of $A$ . For Range Minimum Query, each tree node will contain the value of $getMin(segment)$ (the index of the minimum value in the node’s segment of the array).

Now, how are nodes and segments assigned? For simplicity, let’s assume that $A$ ‘s length is a power of two:

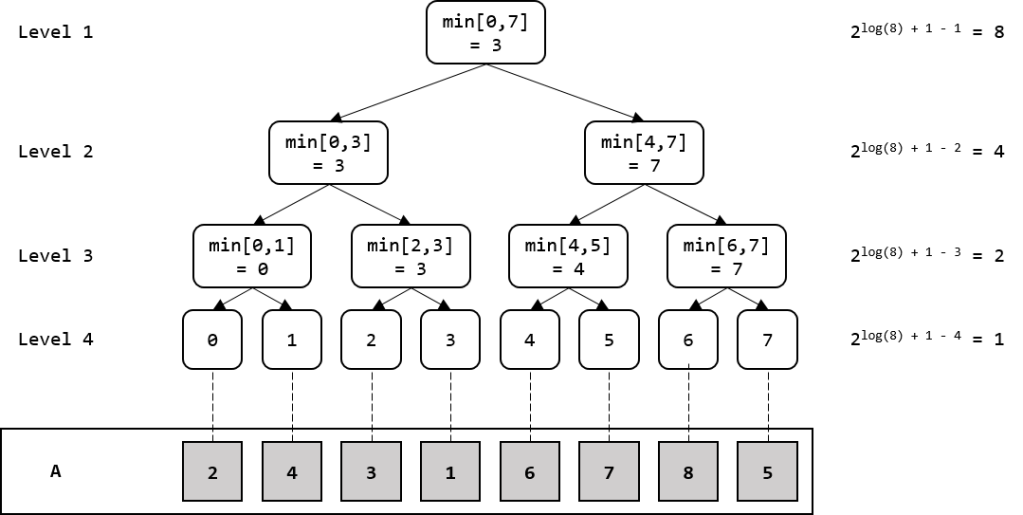
Starting at the lowest level of the tree, we’ll have $N$ leaf nodes each representing an element of $A$ . As shown in the following figure, if we label leaf nodes from $0$ to $N - 1$ from left to right, each node $i$ will contain the value $i$ .
For each internal node $node$ starting from the bottom, we compute $node.value$ as follows: $node.value = m, A[m] = min\{A[node.left.value], A[node.right.value]\}$ . Meaning, a parent node $node$ will get the value of one of its children such that $A[node.value]$ is minimum.
Since this is a binary tree with the last level having $N$ nodes, the tree will have the height of $log(N) + 1$ . Level $0$ will have one node, the root, which holds $getMin(0, N - 1)$ . This means that each node on a level $L$ will represent a segment of length $2^{log(N) + 1 - L}$ .

The implementation is going to be straight forward from here on. We’ll represent the tree as an array tree of length 2 << ceil(log2(N + 1)). Node i has a left child 2 * i and a right child 2 * i + 1. On an update(i), we’ll traverse the tree from top to bottom, change array value at when we reach the leaf i, and update the tree as we go back up. On a getMin(range), we’ll recurse from root until we visit all maximal sub-segments of the range and return the required value. Here’s an implementation in C++ with this tutorial as a reference:

#include <iostream>
#include <vector>
#include <cstring>
#include <cmath>
using namespace std;

class segTree {
    // O(n)
    int *array, *tree;
    int arrayLen, treeLen;

    // O(n)
    void initialize(int node, int b, int e) {
        if (b == e)
            tree[node] = b;
        else {
            // recurse
            initialize(2 * node, b, (b + e) / 2);
            initialize(2 * node + 1, (b + e) / 2 + 1, e);
            // update value
            if (array[tree[2 * node]] <= array[tree[2 * node + 1]])
                tree[node] = tree[2 * node];
            else
                tree[node] = tree[2 * node + 1];
        }
    }
public:
    segTree(int *array, int arrayLen) {
        this->arrayLen = arrayLen;
        this->array = array;
        this->treeLen = 2 << (int)ceil(log2(arrayLen));
        cout << "treeLen=" << treeLen << endl;
        this->tree = new int[treeLen];
        memset(tree, -1, sizeof(int) * treeLen);
        initialize(1, 0, arrayLen - 1);
    }

    // O(log n)
    void update(int i, int v, int node = 1, int b = 0, int e = 0) {
        e = arrayLen - 1 - e;
        if (b == e) {
            array[i] = v;
        } else {
            int mid = (b + e) / 2;
            if (i <= mid)
                update(i, v, 2 * node, b, arrayLen - 1 - mid);
            else
                update(i, v, 2 * node + 1, mid + 1, arrayLen - 1 - e);
            if (array[tree[2 * node]] <= array[tree[2 * node + 1]])
                tree[node] = tree[2 * node];
            else
                tree[node] = tree[2 * node + 1];
        }
    }

    // O(log n)
    int query(int i, int j, int node = 1, int b = 0, int e = 0) {
        e = arrayLen - 1 - e;
        // bad interval
        if (i > e || j < b)
            return -1;
        // good interval
        if (b >= i && e <= j)
            return tree[node];
        // partial interval
        int left = query(i, j, 2 * node, b, arrayLen - 1 - (b + e) / 2);
        int right = query(i, j, 2 * node + 1, (b + e) / 2 + 1, arrayLen - 1 - e);
        if (left == -1)
            return tree[node] = right;
        if (right == -1)
            return tree[node] = left;
        if (array[left] <= array[right])
            return tree[node] = left;
        return tree[node] = right;
    }
};

int main() {
    int A[10] = { 2, 4, 3, 1, 6, 7, 8, 9, 1, 7 };
    segTree t(A, 10);
    cout << "getMin(0, 4) = " << t.query(0, 4) << endl;
    t.update(1, 0);
    cout << "getMin(0, 4) = " << t.query(0, 4) << endl;
    t.update(0, -1);
    cout << "getMin(0, 4) = " << t.query(0, 4) << endl;
    return 0;
}

1111 – Trash Removal

February 22, 2013February 20, 2013 by MSiddeek, posted in Algorithms, Geometry, Problems

You’re required to find the minimum width of an arbitary polygon. The solution can be found in two steps:

Find a convex hull that contains the polygon.
Find it’s minimum width. I choose the Rotating Calipers to do this.

C++ rank 43:

#include <algorithm>
#include <iostream>
#include <complex>
#include <vector>
#include <limits>
#include <cmath>
using namespace std;

typedef long double gtype;
const gtype pi = M_PI;
typedef complex<gtype> point;
#define x real()
#define y imag()
#define polar(r, t) polar((gtype) (r), (t))
// vector
#define rot(v, t) ( (v) * polar(1, t) )
#define crs(a, b) ( (conj(a) * (b)).y )
#define dot(a, b) ( (conj(a) * (b)).x )
#define pntLinDist(a, b, p) ( abs(crs((b)-(a), (p)-(a)) / abs((b)-(a))) )
bool cmp_point(point const& p1, point const& p2) {
	return p1.x == p2.x ? (p1.y < p2.y) : (p1.x < p2.x);
}

// O(n.log(n)) - monotone chain
vector<point> mcH;
void monotoneChain(vector<point> &ps) {
	vector<point> p(ps.begin(), ps.end() - 1);
	int n = p.size(), k = 0;
	mcH = vector<point>(2 * n);
	sort(p.begin(), p.end(), cmp_point);
	for (int i = 0; i < n; i++) {
		while (k >= 2 && crs(mcH[k - 1] - mcH[k - 2], p[i] - mcH[k - 2]) <= 0)
			k--;
		mcH[k++] = p[i];
	}
	for (int i = n - 2, t = k + 1; i >= 0; i--) {
		while (k >= t && crs(mcH[k - 1] - mcH[k - 2], p[i] - mcH[k - 2]) <= 0)
			k--;
		mcH[k++] = p[i];
	}
	mcH.resize(k);
}
// O(n) - rotating calipers (works on a ccw closed convex hull)
gtype rotatingCalipers(vector<point> &ps) {
	int aI = 0, bI = 0;
	for (size_t i = 1; i < ps.size(); ++i)
		aI = (ps[i].y < ps[aI].y ? i : aI), bI = (ps[i].y > ps[bI].y ? i : bI);
	gtype minWidth = ps[bI].y - ps[aI].y, aAng, bAng;
	point aV = point(1, 0), bV = point(-1, 0);
	for (gtype ang = 0; ang < pi; ang += min(aAng, bAng)) {
		aAng = acos(dot(ps[aI + 1] - ps[aI], aV)
			/ abs(aV) / abs(ps[aI + 1] - ps[aI]));
		bAng = acos(dot(ps[bI + 1] - ps[bI], bV)
			/ abs(bV) / abs(ps[bI + 1] - ps[bI]));
		aV = rot(aV, min(aAng, bAng)), bV = rot(bV, min(aAng, bAng));
		if (aAng < bAng)
			minWidth = min(minWidth, pntLinDist(ps[aI], ps[aI] + aV, ps[bI]))
			, aI = (aI + 1) % (ps.size() - 1);
		else
			minWidth = min(minWidth, pntLinDist(ps[bI], ps[bI] + bV, ps[aI]))
			, bI = (bI + 1) % (ps.size() - 1);
	}
	return minWidth;
}

int main() {
	int caseI = 0, n;
	vector<point> p;
	cout.precision(2);
	while (cin >> n && n) {
		p.clear(), p.resize(n + 1);
		// input
		for (int i = 0; i < n; ++i)
			cin >> p[i].x >> p[i].y;
		p[n] = p[0];
		// solve
		monotoneChain(p);
		if (caseI)
			cout << endl;
		cout << "Case " << ++caseI << ": " << fixed << rotatingCalipers(mcH);
	}
	return 0;
}

10480 – Sabotage

February 22, 2013February 20, 2013 by MSiddeek, posted in Algorithms, Graph, Problems

You’re given a specification of a country’s network connnection. Find the connections that must be destroyed to speparate two cities in this network. Make sure the connections you pick are of lowest sabotage cost.

This is a minimum cut prolem which can be solved using the Edmond-Karp maximum flow algorithm.

#include <algorithm>
#include <cstring>
#include <cstdio>
#include <limits>
#include <queue>
#include <map>
using namespace std;

#define N 60
typedef map<int, int>::iterator itr;
map<int, int> res[N];
int parent[N], n, s = 0, t = 1;

bool bfs() {
	queue<int> q;
	q.push(s);
	memset(parent, -1, sizeof parent);
	parent[s] = s;
	while (q.size()) {
		int u = q.front();
		q.pop();
		if (u == t)
			return true;
		for (itr it = res[u].begin(); it != res[u].end(); ++it)
			if (parent[it->first] == -1 && it->second > 0)
				parent[it->first] = u, q.push(it->first);
	}
	return false;
}

int maxFlow() {
	int mf = 0, f, v;
	while (bfs()) {
		// min
		v = t;
		f = numeric_limits<int>::max();
		while (parent[v] != v)
			f = min(f, res[parent[v]][v]), v = parent[v];
		// update
		v = t;
		mf += f;
		while (parent[v] != v)
			res[parent[v]][v] -= f, res[v][parent[v]] += f, v = parent[v];
	}
	return mf;
}

int main() {
	int m;
	while (scanf("%d %d", &n, &m) == 2 && (n || m)) {
		// init
		for (int i = 0; i < n; ++i)
			res[i].clear();
		// input
		for (int a, b, c; m; --m)
			scanf("%d %d %d", &a, &b, &c), res[--a][--b] = c, res[b][a] = c;
		// solve
		maxFlow();
		for (int i = 0; i < n; ++i)
			if (parent[i] != -1)
				for (itr it = res[i].begin(); it != res[i].end(); ++it)
					if (parent[it->first] == -1)
						printf("%d %d\n", i + 1, it->first + 1);
		printf("\n");
	}
	return 0;
}

10034 – Freckles

September 9, 2012 by MSiddeek, posted in Algorithms, Graph, Problems

A Minimum Spanning Tree graph problem.
You’re to find the MST that connects n 2D-points. To apply the MST algorithm, we need a graph first. The graph is built by connecting all the nodes (n(n+1)/2 edges each has weight equal to the distance between its ends). C++ implementation using Kruskal’s MST:

#include <algorithm>
#include <complex>
#include <cstdio>
#include <vector>
#include <map>
using namespace std;

typedef double gtype;
typedef complex<gtype> point;
#define x real()
#define y imag()

vector<pair<gtype, pair<int, int> > > edges;

vector<int> parent;
#define setClear() parent.clear()
#define setMake() parent.push_back(parent.size())
#define setUnion(i, j) parent[setFind(i)] = setFind(j)
int setFind(int i) {
	if (parent[i] == i)
		return i;
	return parent[i] = setFind(parent[i]);
}

int main() {
	int nCase, nP;
	point p[100];
	scanf("%d", &nCase);
	while (nCase--) {
		// input
		scanf("%d", &nP);
		setClear();
		edges.clear();
		for (int i = 0; i < nP; ++i)
			setMake();
		for (int i = 0; i < nP; ++i) {
			scanf("%lf %lf", &p[i].x, &p[i].y);
			for (int j = 0; j < i; ++j)
				edges.push_back(make_pair(abs(p[i] - p[j]), make_pair(i, j)));
		}
		// kruskal's bfs
		int edgesMST = 0;
		gtype weightMST = 0;
		sort(edges.begin(), edges.end());
		while(edgesMST < nP - 1) {
			pair<gtype, pair<int, int> > e = edges[0];
			edges.erase(edges.begin());
			if(setFind(e.second.first) != setFind(e.second.second)) {
				setUnion(e.second.first, e.second.second);
				weightMST += e.first;
				edgesMST++;
			}
		}
		// output
		printf("%.2f\n", weightMST);
		if(nCase)
			printf("\n");
	}
	return 0;
}

10263 – Railway

August 7, 2012 by MSiddeek, posted in Algorithms, Geometry, Problems

A geometry distance computation problem.
You’re given N broken lines and a point M. Find the point S on the broken line that’s nearest to M.
The required point can be either on one end of a broken line segment, or it can be M’s projection on that segment. The rest is mere find-minimum computation. C++ implementation:

#include <iostream>
#include <complex>
#include <limits>
using namespace std;

typedef long double gtype;
#define inRange(a, b, p, e) ( (p) >= min(a, b) - (e) && (p) <= max(a, b) + (e))
const gtype len_before_point_digits = 1E8;
const gtype epsLen = numeric_limits<gtype>::epsilon() * len_before_point_digits;
typedef complex<gtype> point;
#define x real()
#define y imag()
#define crs(a, b) ( (conj(a) * (b)).y )
#define intrN(a, b, p, q) ( crs((p)-(a),(b)-(a)) * (q) - crs((q)-(a),(b)-(a)) * (p) )
#define intrD(a, b, p, q) ( crs((p)-(a),(b)-(a)) - crs((q)-(a),(b)-(a)) )
#define pointDist(a, b, p) ( crs((b)-(a), (p)-(a)) / abs((b)-(a)) )
#define perp(p) ( point(-(p).y, (p).x) )
#define inRect(a, b, p, e) ( inRange((a).x, (b).x, (p).x, e) && inRange((a).y, (b).y, (p).y, e) )

void min(point* station, point p0, point p1, point m, gtype* minD) {
	// end points
	gtype d = abs(p1 - m);
	if (d <= *minD) {
		*minD = d;
		*station = p1;
	}
	// perp distance
	d = abs(pointDist(p0, p1, m));
	point v = perp(p1 - p0) + m;
	point r = intrN(p0, p1, m, v) / intrD(p0, p1, m, v);
	if (d <= *minD && inRect(p0, p1, r, epsLen)) {
		*minD = d;
		*station = r;
	}
}

int main() {
	cout.precision(4);
	int n;
	point m, start, p[2], station;
	while (cin >> m.x >> m.y) {
		gtype minD = numeric_limits<gtype>::max(), d;
		cin >> n;
		cin >> p[0].x >> p[0].y;
		start = point(p[0]);
		// start point
		d = abs(p[0] - m);
		if (d <= minD) {
			minD = d;
			station = p[0];
		}
		// broken line
		for (int i = 0; i < n; ++i) {
			cin >> p[1].x >> p[1].y;
			min(&station, p[0], p[1], m, &minD);
			p[0] = point(p[1]);
		}
		// end point
		min(&station, p[0], start, m, &minD);
		cout << fixed << station.x << endl << station.y << endl;
	}
	return 0;
}

Tag: minimum